For GUI development, we often start with controls (or widgets) that user interact with and it’ll emit/run the callback function we registered for the event when the event happens.
Most of the time we just want to read the state/properties of certain controls, process them, and update other controls to show the result. Model-View-Controller (MVC) puts strict boundaries between interaction, data processing and display.
The most common schematic for MVC is a circle showing the cycle of Controller->Model->View, but in practice, it’s the controller that’s the brains. The view can simultaneously accept user interactions, such as a editable text box or a list. The model usually don’t directly update the view directly on its own like the idealized diagram.
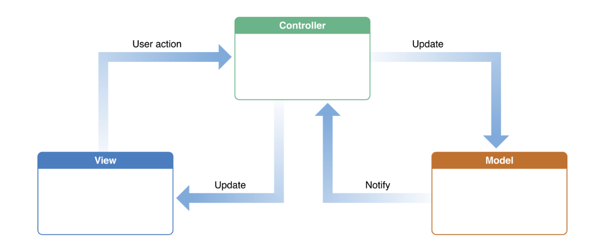
With MVC, basically we are concentrating the control’s callbacks to the controller object instead of just letting each control’s callback interact with the data store (model) and view in an unstructured way.
When learning Flutter, I was exposed to the Redux pattern (which came from React). Because the tutorials was designed around the language features of Dart, the documentation kind of obscured the essence of the idea (why do we want to do this) as it dwelt on the framework (structure can be refactored into a package). The docs talked a lot about boundaries but wasn’t clearly why they have to be meticulously observed, which I’ll get to later.
The core inspiration in Redux/BLoC is taking advantage of the concept of ‘listening to a data object for changes’ (instead of UI controls/widget events)!
Instead of having the UI control’s callback directly change other UI control’s state (e.g. for display), we design a state vector/dictionary/struct/class that holds contents (state variables) that we care. It doesn’t have to map 1-1 to input events or 1-1 to output display controls.
When an user interaction (input) event emitted a callback, the control’s callback do whatever it needs to produce the value(s) for the relevant state variable(s) and change the state vector. The changed state vector will trigger the listener that scans for what needs to be updated to reflect the new state and change the states of the appropriate view UI controls.
This way the input UI controls’ callbacks do not have to micromanage what output UI controls to update, so it can focus on the business logic that generates the content pool that will be picked up by the view UI controls to display the results. In Redux, you are free to design your state variables to match more closely to the input data from UI controls or output/view controls’ state. I personally prefer a state vector design that is closer to the output view than input controls.
The intuition above is not the complete/exact Redux, especially with Dart/Flutter/React. We also have to to keep the state in ONE place and make the order of state changes (thus behavior) predictable!
- Actions and reducers are separate. Every input control fires a event (action signal) and we’ll wait until the reducers (registered to the actions) to pick it up during dispatch() instead of jumping on it. This way there’s only ONE place that can change states. Leave all the side effects in the control callback where you generate the action. No side effects (like changing other controls) allowed in reducers!
- Reducers do not update the state in place (it’s read only). Always generate a new state vector to replace the old one (for performance, we’ll replace the state vector if we verified the contents actually changed). This will make timing predictable (you are stepping through state changes one by one)
In Javascript, there isn’t really a listener actively listening state variable changes. Dispatch (which will be called every time the user interacts using control) just runs through all the listeners registered at the very end after it has dispatched all the reducers. In MATLAB, you can optionally set the state vector to be Observable and attach the change listener callback instead of explicitly calling it within dispatch.
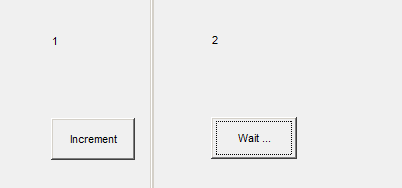
Here is an example of a MATLAB class that captures the spirit of Redux. I added a 2 second delay to emulate long operations and used enableDisableFig() to avoid dealing with queuing user interactions while it’s going through a long operation.
classdef ReduxStoreDemo < handle
% Should be made private later
properties (SetAccess = private, SetObservable)
state % {count}
end
methods (Static)
% Made static so reducer cannot call dispatch and indirectly do
% side effect or create loops
function state = reducer(state, action)
% Can use str2fun(action) here or use a function map
switch action
case 'increment'
fprintf('Wait 2 secs before incrementing\n');
pause(2)
state.count = state.count + 1;
fprintf('Incremented\n');
end
end
end
% We keep all the side-effect generating operations (such as
% temporarily changing states in the GUI) in dispatch() so
% there's only ONE PLACE where state can change
methods
function dispatch(obj, action, src, evt)
% Disable all figures during an interaction
figures = findobj(groot, 'type', 'figure');
old_fig_states = arrayfun(@(f) enableDisableFig(f, 'off'), figures);
src.String = 'Wait ...';
new_state = ReduxStoreDemo.reducer(obj.state, action);
% Don't waste cycles updating nops
if( ~isequal(new_state, obj.state) )
% MATLAB already have listeners attached.
% So no need to scan listeners like React Redux
obj.state = new_state;
end
% Re-enable figure obj.controls after it's done
arrayfun(@(f, os) enableDisableFig(f, os), figures, old_fig_states);
src.String = 'Increment';
end
end
methods
function obj = ReduxStoreDemo()
figure();
obj.state.count = 0;
h_1x = uicontrol('style', 'text', 'String', '1x Box', ...
'Units', 'Normalized', ...
'Position', [0.1 0.3, 0.2, 0.1], ...
'HorizontalAlignment', 'left');
addlistener(obj, 'state', ...
'PostSet', @(varargin) obj.update_count_1x( h_1x , varargin{:}));
uicontrol('style', 'pushbutton', 'String', 'Increment', ...
'Units', 'Normalized', ...
'Position', [0.1 0.1, 0.15, 0.1], ...
'Callback', @(varargin) obj.dispatch('increment', varargin{:}));
% Force trigger the listeners to reflect the initial state
obj.state = obj.state;
end
end
%% These are 'renders' registered when the uiobj.controls are created
% Should stick to reading off the state. Do not call dispatch here
% (just leave it for the next action to pick up the consequentials)
methods
% The (src, event) is useless for listeners because it's not the
% uicontrol handle but the state property's metainfo (access modifiers, etc)
function update_count_1x(obj, hObj, varargin)
hObj.String = num2str(obj.state.count);
end
end
end
![]()