Complex number manipulations are prevalent through the entire ‘Signals and Systems’ course and everywhere that uses the concepts. You won’t get anywhere without it. You need to get so comfortable with it that Chapter 1 of Churchill’s Complex Variables and Applications is child’s play.
Jargon in complex numbers goes under many different names. Remember as many of them as you can since different books will use different terminologies. Some might actually help you to grasp the concepts better. I’ll use them interchangeably without hesitation.
- [Magnitude] radius, length, modulus
- [Phase] angle, direction, argument
- [Cartesian Coordinates] rectangular coordinates
Before we get to properties, you’ll need to have the following intuition in mind so you can easily prove the properties in your head:
- Conjugation flips your the complex number upside down along the real plane.
It reverse the angles and flips the sign of the imaginary part. - Unit circle
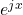 has a radius of
has a radius of 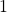 everywhere (
everywhere (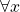 ) . Mathematically
) . Mathematically 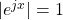 so you don’t have to worry about scaling when you work with the phase.
so you don’t have to worry about scaling when you work with the phase. 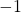 is a phase change of
is a phase change of 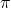 , aka
, aka 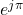 .
. 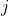 is a
is a 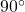 or
or 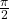 phase shifter.
phase shifter.- Multiplying with non-zero phase rotates the complex number (interpreted as a vector) anti-clockwise (i.e. adding the angles).
The main use of different coordinate systems is to decouple the parameters so you can vary one parameter without changing the rest, which makes visualization or manipulations much easier. Cartesian coordinates decouples real and imaginary parts while polar coordinates decouples length and direction.
In general, polar coordinates are often most helpful for visualizing the ideas (and multiplicative operations) while rectangular coordinates are better for additive manipulations.
Remember ALL of the following properties by heart:
Conjugation distributes both additively ![]() and multiplicatively
and multiplicatively ![]() :
:
![]()
Magnitude distributes ONLY multiplicatively ![]()
![]()
Unless you can guarantee the all complex numbers point in the same direction (same phase, or collinear), adding them might have a cancelling effect. One trivial example: ![]() , but
, but ![]() . Clearly magnitude operator does not distribute additively. The relationship is in fact expressed in terms of triangle inequality:
. Clearly magnitude operator does not distribute additively. The relationship is in fact expressed in terms of triangle inequality:
![]()
Squared magnitude can be expressed as a product of the complex number itself multiplied by its conjugate:
![]()
This can be interpreted in both rectangular (Cartesian) coordinates and polar coordinates:
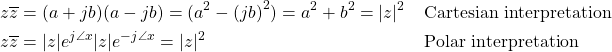
Most of the slick tricks in the class will require this:
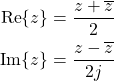
The most common (and handy) use of this decomposition:
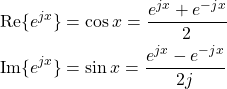
With this, deriving product to sum formula in high school trigonometry becomes a trivial algebra problem of multiplying exponents!
![]()