Category Archives: Economics

Mathematics of calculating overheads to charge

Posted on by
Reply

It’s very common to have a percentage fee (called tax rate below) slapped on our earnings:

  • Commissions (e.g. eBay final value fees)
  • Sales Tax
  • Incremental income taxable within the same bracket.

Many adults cannot directly figure out how much EXTRA do they need to earn to get the target amount of that are rightfully theirs (after fees).

They are missing out these handy intuitions:

  • If your EXTRA earnings are taxed at 40%, not wasting an extra $100 is almost as good as earning $166.67!
  • You always undercharge the fee overhead if you just multiply your target amount with it (intuitive but WRONG). The amount you get shortchanged goes up like a rocket for rates past 10%!

All you need is grade school math to figure it out, but the results are highly non-linear and are not easy to remember. This means the tutorial below makes an excellent discussion material to motivate mathematics education in grade school!

If you want to copy or use the materials, just remember to reference “Rambling Nerd with a Plan” blog page or “Humgar LLC”. You don’t have to ask and you are welcome. I certainly appreciate comments about this tutorial.

Before I start, hints for working with percentages:

  • divide percentages by 100. Think multipliers/factors in your head.
  • a factor of 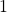1 represents the full amount
  • division by 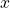x is multiplication by reciprocal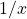 1/x
  • preferably work in terms of shrink/expand factors (multiplications only) over the FULL amount, rather than working out the excesses (additions/subtractions)

Assigning intuitive names are very important for interpreting algebraic expressions with familiar life concepts!

Let’s define these variables first:

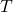  • T is the target price you want to get AFTER the fees
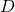  • D is the damage you should charge
  • r is the rate (fee/tax percentages)
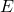  • E is the excess that goes to the fee/tax collector

These derived variables will be discussed in the body of the tutorial

  • s is the shrinkage (multiplier), where

        \[s\equiv(1-r)\]

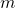  • m is the magnifier (multiplier),

        \[m\equiv\frac{1}{s}\]

  • c is the compensation (multiplier) for billing,

        \[c=m-1\]

If somebody pays you the total damage D before tax/fees (at rate  r), you are home free with T after subtracting the fees D \times r from D

    \[D - rD = (1-r)D \equiv sD = T\]

In other words, you the FULL damages gets shrunk by a factor s \equiv (1-r) which becomes the target amount T you get to keep for yourself.

Don’t be scared by the algebra! It’s just the other way of saying, if your tax rate is 30%, it means you get to keep 70% of your income, because 100%-30% = 70%, so the shrinkage s is 0.7. 

Since you have the target price T in mind and want to undo the shrinkage (multiplication) to calculate the full amount you should charge D, you divide the target price by the T by the same factor to magnify it back:

    \[D = \frac{T}{s} = \frac{T}{1-r}\]

It is NEVER helpful to directly multiply the fee/tax percentage with the target price T like what most people would intuitively do. We can think of the division above as multiplying by the reciprocal of the loss factor s or (1-r), which we will call m the magnifier:

    \[m = \frac{1}{s} = \frac{1}{1-r}\]

An alternative view is to break the damage D into target price T along with excess E to bill the customers for the fees/taxes (which goes to the collector):

    \[D = T + E\]

My preferred way to calculate the excess is simply compute D first by finding calculating the magnifier m, or simply dividing the target price T by the shrinkage s

    \[D = mT = \frac{T}{s} = \frac{T}{1-r}\]

then subtract the target price T from the damage D to get the excess:

    \[E \equiv D-T\]

which you can write it in terms of target price T which you know so you don’t have to work out the total damages D first:

    \[E \equiv D - T = mT - T = T(m-1)\]

We can define compensation (multiplier) c as how much you should multiply the target price T with:

    \[c \equiv m-1\]

to recover your fee/tax costs E:

    \[E = cT\]

e.g. if you need to charge the customer 1.43 times to breakeven after fees (given a 30% tax/fees rate), the overhead ‘item’ on the bill should be 0.43 (43%) of the target price. For a $100 item, you’ll need to bill your customer $43 more just to cover a 30% fees.

In summary, we have

    \[P \equiv T + E = (1+c)T\]

with c that can be figured out quickly as

    \[c = \frac{r}{s}\]

where r and s are both bounded between 0 and 1 which adds up to 1:

    \[r + s = 1\]

Take an example of 30% tax rate (r=0.3), the shrink is 70% (s=0.7), because the factors are complements to each other which adds up to 1.

    \[0.3 + 0.7 = 1\]

If you want to write it all in terms of shrinkage  s:

    \[c = \frac{1}{s}-1 = \frac{1-s}{s}\]

Since 1-s = r, we can rewrite the compensation (factor) in these complement terms (r,s), which I think it’s the easiest way to remember:

    \[c = \frac{r}{s}\]

or simply the rate r divided by shrinkage s,

You can also write it in terms of fees/tax rate r in full:

    \[c = \frac{r}{1-r}\]

e.g. if you have a 30% tax rate , you can find the compensation (factor) c by calculating 3/7, because it’s simply 30% over 70%.

To estimate the overhead charge to offset the fee percentage, or compensation c by multiplying with the target price T:

WRONG way

    \[r\]
CORRECT way

    \[\frac{r}{1-r}\]

The gap (amount you get shortchanged by computing compensation c wrong) is:

    \[g \equiv c-r = \frac{r}{1-r}-r = \frac{r^2}{1-r}\]

The numbers look close enough (for the intuitive but wrong way) when it’s like around 10%, but your loss (overheads not charged) shoots up (non-linearly) as the fee/tax percentage goes up beyond 10%!

Fee percentage

    \[r\]

 Correct overhead % to charge

    \[c = \frac{r}{1-r} = \frac{r}{s}\]

 Undercharged

    \[\frac{r^2}{1-r}\]
5% 5.26% 0.26%
10% 11.11% 1.1%
20% 25% 5%
30% 42.86% 12.86%
40% 66.67% 26.67%
50% 100% 50%

Intuitively, you need to charge DOUBLE the target price if half of it gets taxed to breakeven, NOT adding half of the target price as the overhead! The FULL target price itself is the right overhead to charge for a 50% tax rate!

Since the numerator r is bounded because 0 \leq r < 1, the denominator (1-r) can blow up (the overhead needed to charge your customer) as it gets small (i.e. high tax/fee percentage). Here’s a plot of

    \[\frac{1}{1-r}\]

.

e.g. A 66.6% imports tax rate means giving two cars to the government when you import one!

To push it to the extreme, 90% tax rate would mean 900% overhead, which means if you buy one car, you give the government 9 cars, assuming they don’t tax themselves. Your estimates are off by 10 times if you use the wrong method to compute the excess E making up for the tax that gets charged.

If people can think in terms of the excess you will need to earn EXTRA to offset the tax rate, you will think twice about letting the government dip in another 2% or so. That’s why welfare-state through taxes can be highly counter-productive when it get past certain point.

Advanced analysis for the intrigued

Just for fun, let’s investigate the impractical case (communist tyrants) when tax rates gets to 100% and above (r \geq 1):

Fee percentage

    \[r\]

 Correct overhead % to charge

    \[c = \frac{r}{1-r} = \frac{r}{s}\]

 Undercharged

    \[\frac{r^2}{1-r}\]
\vdots \vdot \vdots
90% 900% 810%
100% \infty \infty
200% -200% -400%
300% -150% -450%
\vdots \vdot \vdots
\infty -100%
 –\infty

When charged 100% tax rate, the government seize any gains from your production. There’s never enough overhead you can charge your customer to breakeven.

The more perverted case is what happens when you go above 100%, say at 200% tax rate? When you sell $100 worth of stuff, you pay the government $200 to do so. You are paying a $100 penalty to work/produce $100 for the government. Twisted!

Then how do we explain the negative numbers in the compensation (factor) c? In reality, it means you ALWAYS make a loss no matter what. There’s no way you can bill your customer to make up for the loss.

In the unrealistic (unicorn) case, if the benevolent crazy dictator is willing and able to compensate your losses (at the sales tax rate), aka giving you money back every time you lose money,

    \[P = (1+c)T\]

means the the magnifier m \equiv (1+c) < 0 for sure when r \ge 1. It’s illustrated in the graph as a deadzone

    \[-1 < \frac{r}{1-r} < 0\]

:

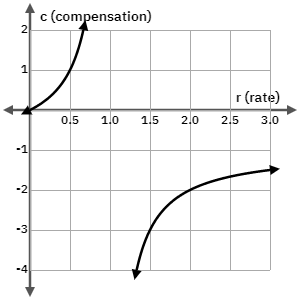which you can verify the same by solving this inequality

    \[-1 < \frac{r}{1-r} \leq 0\]

and realize you get r-1 \ge r when (1-r) \leq 0, which boils down to saying -1 \ge 0 which is a contradiction.

That means to achieve target earnings T under tax rates above 100%, you should charge the customer negative amounts (i.e. giving away goods + money) in order to get the negative taxes (subsidy).

e.g. At 300% tax rate (r=3), it your sticker price (also target price) is $100, you’ll need to GIVE the customer $50 so the government will triple match your loss as a subsidy (which is $150), which is enough to cover the $50 giveaway (to the customer) plus the $100 so you’ll breakeven.

Having negative tax (subsidy) is a perverse incentive. Forget about maintaining a target earning (same as the original sticker price for the goods you are selling), just lose (give away) money as fast as you can to suck up as much subsidy as you can before the system collapse.

I still fondly recall my economics 301 (intermediate microeconomics professors) James Montgomery saying that “if you can graph it, it can possibly happen” in the lecture.

Even more sophisticated math for the geeks

Remember from above, the magnification factor m can be rewritten as the reciprocal of shrinkage factor s?

    \[m = \frac{1}{s} = \frac{1}{1-r}\]

which reminds me of geometric series

    \[\frac{1}{1-r} = 1 + r + r^2 + r^3 + \cdots}\]

given |r| < 1? For non-perverted cases, we are considering 0 \leq r < 1, which is well within the domain.

This gives an idea of approximating the compensation factor c:

    \[m \equiv 1+c = 1 + r + r^2 + r^3 + \cdots\]

which after taking 1 off both sides:

    \[c = r + r^2 + r^3 + \cdots\]

This explains exactly why people are wrong to just assume c is just r, because their false intuition kept ONLY the first order term in the power series approximation!

The gap (how much they are off with the WRONG way), is

    \[g \equiv c-r = \frac{r^2}{1-r} = r^2 + r^3 + \cdots\]

So while 0.1^2 dies fast enough (0.01) by 2nd order term, 0.9^2=0.81, 0.9^3 = 0.729 … are still very significant up to say 6th order term which makes it off by a factor of 8.1.

Yes, you are off by 1% when the tax rate is 10%, but you can be wrong by a factor of 8.1 times if you just multiplied the tax rate r with the target price T to estimate the amount of excess E to collect to make up for the fees!

Summary

  • The total damage (bill) you should charge your customer can be calculated by dividing the target amount (of money you want to home free with) by the shrinkage, which is (1 – tax rate). e.g. 30% tax rate means 70% shrinkage. Divide the target by 0.7 to get the final bill
  • A shortcut to calculate how much you should put in (by multiplying with the target price) for an charge item on the bill to make up for the fees is (tax rate)/(shrinkage) e.g. 30% tax rate means 70% shrinkage. Multiply the target by 30/70 (or 3/7, which is 42%) to get the excess which covers the fee.
  • Do NOT attempt to use the rule of thumb to calculate the excess by just multiplying with the tax rate unless it’s 10% or less. The ‘rule of thumb’ assumed 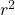r^2 (and thus the higher powers) are insignificant, which is nowhere true for 0.1 and above based on this graph!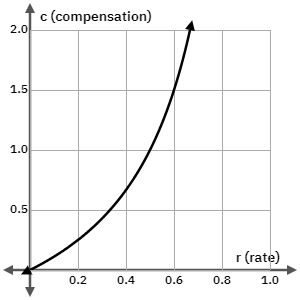

Loading