Dart’s documentation at the time of writing (2021-10-27) is not as detailed as I hoped for so I don’t know if the Lambda (anonymous function) is late-binding or early-binding.
For those who don’t know what late/early-binding is:
| Binding | early | late |
| Expression | closed (closure) | open (not a closure) |
| Self-contained | yes | no |
| Free symbols (relevant variables in outer workspace) | bound/captured at creation (no free symbols) | left untouched until evaluated/executed (has free symbols) |
| Snapshot | during creation | during execution |
Late-binding is almost a always a gotcha as it’s not natural. Makes great Python interview problems since the combination of ‘everything is a reference‘ and ‘reference to unnamed objects‘ spells trouble with lazy evaluation.
I’d say unlike MATLAB, which has a more mature thinking that is not willing to trade a slow-but-right program for a fast-but-wrong program, Python tries to squeeze all the new cool conceptual gadgets without worrying about how to avoid certain toxic combinations.
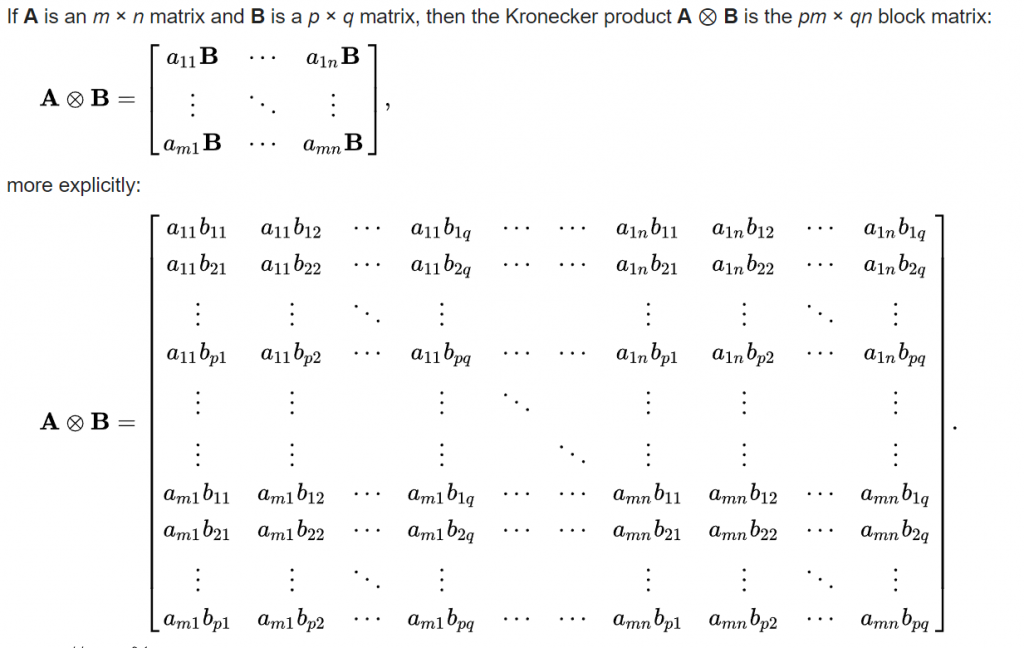
I wrote a small program to find out Dart’s lambda is late-bound just like Python:
void main()
{
int y=3;
var f = (int x) => y+x;
// can also write it as
// f(int x) => y+x;
y=1000;
print( f(10) );
}
| Language | Binding rules for lambda (anonymous functions) |
|---|---|
| Dart | Late binding Need partial application (discussed below) to enforce early binding. |
| Python | Late binding. Can capture (bind early) by endowing running (free) variables (symbols) with defaults based on workspace variables |
| C++11 | Early binding (no access to caller workspace variables not captured within the lambda) |
| MATLAB | Early binding (universal snapshot, like [=] capture with C++11 lambdas) |
I tried to see if there’s a ‘capture’ syntax in Dart like in C+11 but I couldn’t find any.
I also tried to see if I can endow a free symbol with a default (using an outer workspace variable) in Dart, but the answer is no because unlike Python, default value expressions are required to be constexpr (literals or variables that cannot change during runtime) in Dart.
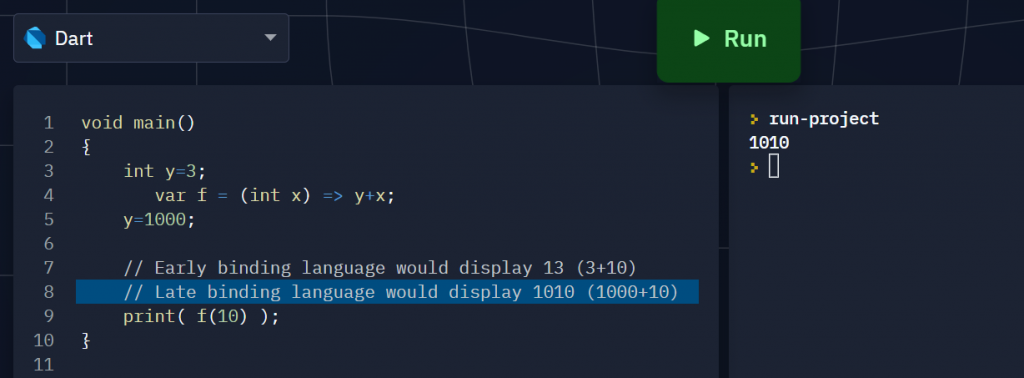
So far the only way to do early binding is with Partial Application (currying is different: it’s doing partial application of multiple variables by breaking it into a cascade of function compositions when you partially substitute one free variable/symbol at a time):
- Add an extra outer function layer (I call it the capture/binder wrapper) putting all free variables you want to bind as input arguments (which shadows the variables names outside the lambda expression if you chose not to rename the parameter variables to avoid conceptual confusion),
- then immediately EVALUATE the wrapper with the with the outer workspace variables (free variables) to capture them into the functor (closed lambda, or simply closure) which binder wrapper spits out.
Note I used a different style of lambda syntax in the partial application code example below
void main()
{
var y=3;
f(int x) => y+x;
// Partial Application
g(int w) => (int x) => w+x;
// Meat: EVALUATING g() AT y saves the content of y in h()
var h = g(y);
y=1000;
// y is free in f
print( f(10) );
// y is not involved in g until now (y=1000)
print( g(y)(10) );
// y is bounded for h when it was still y=3
print( h(10) );
}
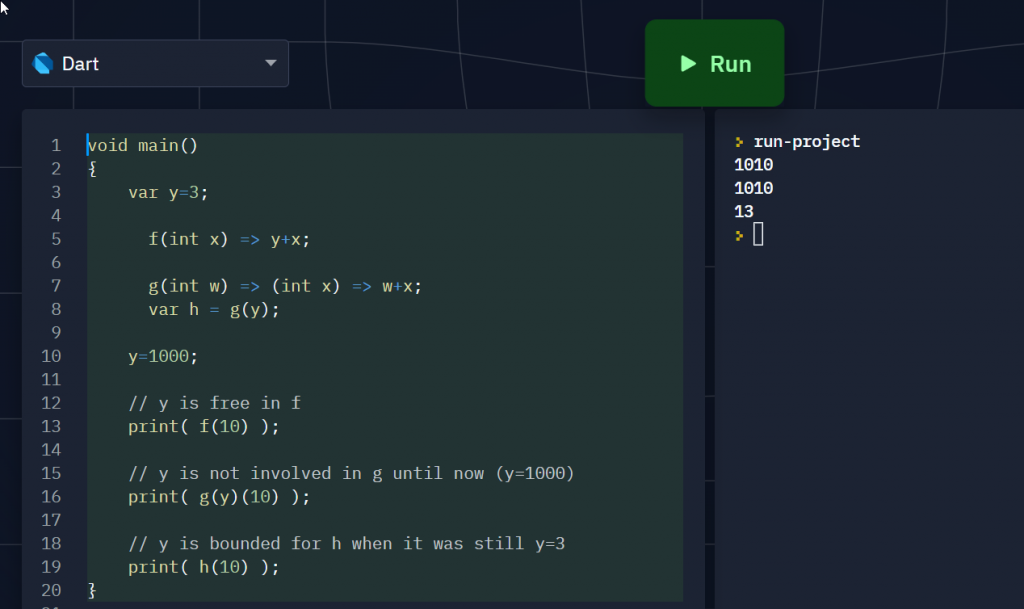
Only h() captures y when it’s still 3. The snapshot won’t happen if you cascade it with other lambda (since the y remains free as they show up in the lambda expression).
You MUST evaluate it at y at the instance you want y captured. In other words, you can defer capturing y until later points in your code, though most likely you’d want to do it right after the lambda expression was declared.
As a side note, I could have used ‘y’ instead of ‘w’ as parameter in the partial application statement
g(int y) => (int x) => y + x
but the ‘y‘ inside g() has shadowed (no longer refers to) the ‘y‘ in the outer workspace!
What makes it confusing here is that quite a few authors think it’s helpful (mnemonics-wise) to use the free variable (outer scope) name you are going to inject into the dummy (argument) as the name of the dummy! This gives the false impression of the variable being free while it’s bounded (through feeding it as a parameter in the wrapper/outer function)!
Scoping rules is a nasty source of confusion in understanding lambda calculus so I decide to give it a different name ‘w‘. I’m generally dismissive of shadowing under any circumstances, to the extent that I find Python’s @ syntactic sugar for decorators shadowing the underlying function which could have been reused somewhere (because it’s implicitly doing f=g(f) instead doing h=g(f). I hate it when you see the function with name f then f was repurposed to not mean the definition of f you saw right below but you have to keep in mind that it’s actually a g(f)). See my rants here.
Notational ambiguity, even if resolvable, is NOT helpful at all here especially when there are so many level of abstractions squeezed into so few symbols! People jumping into learning the subject quickly for the first time should not have unnecessarily keep track of the obscure scoping rules in their head to resolve the ambiguities!
![]()