For the convenience of my customers, I compiled a quickie setup guide so they don’t have the RTFM.
E2050A does not have DHCP. Most likely your network doesn’t have a ancient BOOTP server, so it means you are better off letting E2050A have a static IP address.
The big idea is that you’ll first need to talk to the E2050A, and the only way it can happen is that the computer talking to it has to be on the same subnet (and the corresponding IP address range). Doesn’t matter how you achieve it as long as you keep this in mind. Once you gained access to the router (telnet config screen), you can change the network setting of the E2050A to match whatever network you want to put it on later.
If you don’t know the E2050A’s network configuration, reset it to the default so you have a deterministic starting point and follow the instructions below:
- Reset the instrument to factory state by holding down CONFIG PRESET switch while applying power, because you want to know the IP address for sure so you can get into the instrument.
- The default static IP address is 192.0.0.192, under subnet mask 255.255.255.0
- Most likely your internal network is not 192.0.0.XXX, so you might want to use a computer with a network card (NIC) to talk to the device directly* (point-to-point) first so you can gain entry to the E2050A and change its network configuration.
- The NIC on the computer talking to the E2050A must be set to an IP address in the same subnet. This means only the last (rightmost) group of the NIC’s static IP address can be different. An example for the computer’s NIC static IP setting: 192.0.0.190 with subnet 255.255.255.0.
- Now you can talk to the E2050A directly by addressing 192.0.0.190. If it’s a dedicated computer for an automation set and you don’t want it to talk to the rest of the network, you are done.
I made up 192.0.0.190. Anything from 192.0.0.1 to 192.0.0.254 works. Thou shalt not use 192.0.0.0 (for it is the network identifier) or 192.0.0.255 (for it is the network broadcast address) or 192.0.0.192 (as it conflicts with the E2050A’s IP).
Most likely you will want to put the E2050A on your home/business network for convenience, unless you want to eliminate network security issues. Then you’ll need to follow a few more steps:
- Telnet to the E2050A at 192.0.0.192 to change its static IP address and subnet to fit your network. After saving and rebooting, you must address it with the new IP address you assigned (obviously!).
- Note that the default (SICL) interface name on the E2050A is “hpib”, which is different from E5810A’s default “gpib0”. Either change it on the E2050A (it’s called “hpib-name”) or enter the “hpib” for interface name on Agilent’s I/O suite.
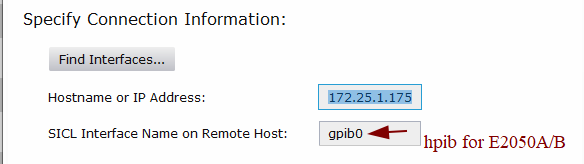
- You can leave the rest of the settings alone in Agilent I/O suite if you want to simply talk (in its raw, instrument-specific GPIB commands) to the unit without using VISA or SICL layers (standardized syntax).
E2050A has the same software communication interface as E5810A, so you can just select E5810A as the remote interface for the E2050A and remember to enter the correct interface name as discussed above.
Note that E2050A does not work properly (won’t detect) on the redesigned Keysight-branded I/O Suite until version 2019. Please either use version 2019 and after OR the older Agilent branded I/O Suite.
I have E2050A as well as E5810A for sale. Please contact me from my business website (www.humgar.com) or my phone 949-682-8145.
* Unless you are using a very ancient computer, the NIC can auto-negotiate direct connection that you can simply use any regular old straight RJ-45 cable. If you have a really old computer, you’ll need a cross-over cable to do point-to-point ethernet.
![]()




