Daily Archives: March 9, 2019

Explain XOR tricks succinctly with two properties Change detector, toggler

Posted on by
Reply

Most teaching materials on XOR starts from its straight definition then a bunch of recipes for exploiting XOR. It is not convenient to remember and not intuitive to come up with new tricks on our own. Instead, I’d like to describe XOR as two intuitive operations:

  1. Change detector (The logic definition itself)
  2. Toggling light switches (Flipping twice undoes it)

The second interpretation (toggling) is actually way more powerful and easy to remember than the first interpretation (definition).

With the toggling interpretation, you don’t have to think hard to come up with the four algebraic properties:

  1. Associativity and commutativity: we only care about whether the individual light switches (bits) are flipped odd (flipped) or even (not-flipped) number of times at the end of the day. When it happens in what order does not matter.
  2. Identity: flipping NONE of the switches (a mask of all 0) leaves it alone
  3. Inverse: pick only the switches that are already turned on (using itself as mask) and flip them (xor) guarantees to turn everything off (0)

The XOR swap trick can be constructed by exploiting the fact that flipping the same switch twice (at any point) reverts it back to where it started:

x y
Start x_0 y_0
Mix y_0 with x_0 x_1 = x_0 \oplus y_0 No info is lost, still have y_0 somewhere to undo if we wish.
The incumbent 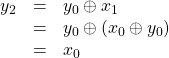y_0 is used to cancel the y_0 inside x_1 to recover x_0 \begin{array}{rcl} y_2 & = & y_0 \oplus x_1 \\ & = & y_0 \oplus (x_0 \oplus y_0)\\ & = & x_0 \end{array} Since y_0 is already saved (mixed with) x_1, we don’t have to worry about losing it as long as we get to our main goal of putting x_0 in y, which will be used as a recovery key later.
Now use the x_0 stored in y_2 to unmix x_1 to recover y_0 \begin{array}{rcl} x_3 & = & x_1 \oplus y_2 \\ & = & (x_0 \oplus y_0) \oplus x_0\\ & = & y_0 \end{array}

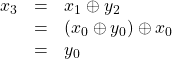Note that this trick is obsolete for modern computer architecture because

  • it enforces strict dependence that kills any predictive pipeline (speedup) in modern computer architecture, and
  • will yield zero all the time if you try to swap with itself in-place (same memory location), which is wrong because you expect the swap to do nothing.

Adding a check for the degenerate case (self-swap) slows the program down even further, making it worse than using a temporary storage for swapping. Therefore there’s no good reason to use it unless you have an exotic use case.

This is mainly used as a teaching device (or homework problem) to teach that XOR-ing even instances of the same variable in the chain cancels it.

 

Loading