Navigating between oscilloscope-land (Volts) and RF-land (dBm)

Have you ever been annonyed by the dBm and V units when you try to measure output from your benchtop signal generator (or arbitrary waveform generator, or ARB) with a spectrum analyzer, or measure a RF signal (sine) generator with an oscilloscope?

TLDR

For $50\Omega$ systems only. The fastest way is to work with squared voltages in linear scale with the provided ‘magic’ scaling factor (10 for amplitude and 20 for rms) and not mess with factorization in the log (dB) or anti-log ( $10^{\frac{\mathrm{dB}}{10}}$ ) process:

P[\mathrm{mW}]=10V_{pp}^2=20V_{rms}^2

\mathrm{dBmW}=\mathrm{dB}\left(10V_{pp}^2\right)=\mathrm{dB}\left(20V_{rms}^2\right)

This happens a lot during calibration. An oscilloscope needs a 500Mhz signal at $600mV_{pp}$ to test if the front-end rolls off too early (i.e. have a lower bandwidth than advertised), yet my $12k RF signal generator (20Ghz sweeper) only does dBm, and in coarse increments of 0.1dBm.

Decibel is supposed to be a dimensionless quantity, aka just a ratio.
The confusion came from people in each field abusing notations by skipping the reference quantity suffix after dB. e.g. RF people write dBW and dBmW (a dimensioned quantity with loaded assumptions of a 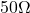$50\Omega$ scaling) as dB and dBm (which would naturally read as a dimensionless ratio)
When RF people talk about decibels, especially when they abuse notations by not mentioning the reference (basis) quantity, you can be pretty sure that they are talking about ratios between power quantites (dBW), not voltage quantities (such as dBV).
There’s no such thing as a 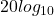$20log_{10}$ decibel unit. It’s always 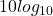$10log_{10}$ dimensionless. The factor of 2 came from the square (power of 2) factoring out of logarithms as a multiple of 2 when ratios of power are expressed as ratios of voltages.
Always work in power ratios to avoid the confusion. dB is dimensionless but often the unspoken rule is that it’s a ratio of power quantities. Routines or formula like mag2db really mean magnitude_squared_in_dB because it’s doing $10log_{10}(A^2)$ .
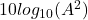The other advantage of actually squaring the term first before taking the log is that you do not have to check the input for negative values as the squaring operation made it absolute value (square). If you are doing a logarithm, an extra multiplication (over an addition) is insignicant in terms of computational burden.
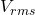$V_{rms}$ maps directly to power quantities, scaled by the impedance (which is typically 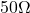$50\Omega$ ). Everything else involves an extra crest factor (which is 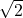$\sqrt{2}$ for sinusoids)

I’ve written an article before detailing the twists that lead to the common confusion (the less-intuitve parts) and the proper derivation. However, I find myself being able to benefit from a quick summary as I had to read the article I’ve written when I need it again.

More importantly, this article shows some menomics shortcut I have for doing these conversions in my head so I can get a ballpark figure without reaching for a calculator or finding the equations for it.

Here is the summary of the last article:

The POWER decibel-speak always assumes a 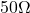$50\Omega$ ‘resistor’ burning the volts, which is related by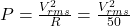 $P=\frac{V_{rms}^2}{R} = \frac{V_{rms}^2}{50}$
Therefore there’s a always factor of 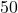$50$ (17dB) from the implied load ‘resistor’ when converting between decibels (power quantity) and voltages.

dBW assumes 1W as basis: how many factors of 10 away from 1W
dBmW assumes 0.001W (1mW) as basis: how many factors of 10 away from 0.001W
dBmW implicitly multiples W by 1000 (add 30dB) to make it mW

30dB translates to 1000x bloat by converting W to mW
17dB translates to the factor of 50 that came from 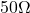$50\Omega$ impedance
To convert dBmW to dB 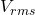$V_{rms}$ , you need to divide by 1000 (-30dB) and multiply by 50 (+17dB), which nets to dividing by 20 (-13dB).

Worked Example 1:

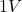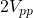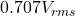$1V$ sinusoid ( $2V_{pp}$ ) is $0.707V_{rms}$ because the crest factor is $\sqrt{2}$ .
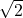Since 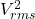$V_{rms}^2$ is 0.5, multiply 20 to get to mW, which is 10mW which is 10dBmW ( $10\log_{10}10$ )

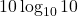Worked Example 2 (reverse of the above):

10dBm(W) sinusoid translates to 10mW (see above). Divide it by 20 gives 0.5 for 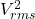$V_{rms}^2$ which you can take the square root to get 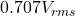$0.707V_{rms}$ which is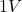 $1V$

My intuitions when working with decibels

dB is just a 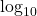$\log_{10}$ multipled by 10 for cosmetics (integers easy to work with and the self-similarity that 10dB is 10 as an anchor point). 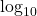$\log_{10}$ is more intuitive to me as this translates directly to how many zeros to add or remove (10s to multiply or divide in 10-base) in linear scale. I divide dB in my head by 10 and read it as ‘it’s off by how many digits’.
Any anchor point
+20dB means multiply 10x in linear voltage scale
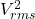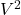+10dB means multiply 10x in linear power ( $V_{rms}^2$ or $V^2$ ) scale
Any anchor point
+6dB means doubling in linear voltage scale
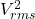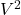+3dB means doubling in linear power ( $V_{rms}^2$ or $V^2$ ) scale
Basically you can break dB numbers into multiple 10dB (tens) and 3dB (doubles) added together (in linear algebra speak, linear combinations) when working in same (power-power, voltage-voltage) scale, and double the dBs to 20dB (tens) and 6dB (doubles) when working from voltage-to-power scale to account for squaring.

Convenient dBmW numbers

My favorite dBmW points are
+10dBmW which is 2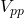 $V_{pp}$ (1V) and
-10dBmW which is 0.2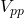 $V_{pp}$ (0.1V)
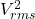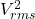mW is divided by 20 to give $V_{rms}^2$ , but $V_{rms}^2$ is multiplied by 2 (due to crest factor) to convert to 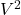$V^2$ , so mW is divided by 10 to go to 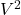$V^2$ , which is easy to work with.
Take the example of 30dBmW which is by definition 1W or 1000mW. Divided by 10 we get 100 in 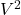$V^2$ , which we take the square root to get 10V
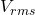$V_{rms}$ is always 3dB above 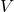$V$ because 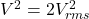$V^2=2V_{rms}^2$ due to crest factor which means the same RMS voltage packs twice the power of the simple voltage amplitude of the same number.
dBmW and dB( 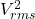$V_{rms}^2$ ) are related by a factor of -13dB (divide by 20, which is -10dB is divided by 10 while -3dB is halving).
for dB( 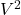$V^2$ ), you divide by 10 (aka -10dB) instead of dividing by 20 (aka -13dB) because the crest factor doubled (+3dB to) the squared voltages when converting from rms to amplitude.

dBmW	V	$V_{pp}$	$V_{rms}^2$	$V_{rms}$
53 (approx)			10000	100
50	100	200
33 (approx)			100	10
31 (approx)			64	8(7.934)
30 (=1W)	10	20
28 (approx)	8(7.9435)	16(15.887)
25 (approx)			16	4
23 (approx)			10
22 (approx)	4(3.981)	8 (7.962)
19 (approx)			4	2
16 (approx)	2	4
13 (approx)			1	1
10	1	2	0.5 half
9 (approx)			0.4
7 (approx)			0.25 quarter	0.5 half
6 (approx)			0.2
4 (approx)	0.5 half	1	0.125(0.12595) 1/8
3 (approx)			0.1
1 (approx)				0.25 quarter
0 (approx)			0.05
-2 (approx)	0.25 quarter	0.5 half
-7 (approx)				0.1
-10	0.1	0.2	0.005
-13 (approx)			0.0025	0.05
-16 (approx)	0.05	0.1	0.00125(0.001256)
-19 (approx)				0.025
-22 (approx)	0.025	0.05
-27 (approx)				0.01
-25 (approx)				0.0125(0.012574)
-28 (approx)	0.0125 (0.01259)	0.025(0.02518)
-30	0.01	0.02
-36 (approx)	0.005	0.01
-47 (approx)				0.001
-50	0.001	0.002

This is a dBm conversion table that you can make in your own head without a calculator or log tables, simply by combinations of doubling/halving and multiply/divide by 10 from the self-similar reference point of 10dBm and for every $V$ , add 3dB to get $V_{rms}$

The other way to think of the why mW (and therefore dBmW) align with $V$ better than $V_{rms}$ is a happy coincidence that the crest factor in the power-voltage relationship just happen to make the scaling factor a $100$ for a $50\Omega$ system which is easier for the $1000$ multiplier to divide by

\frac{P[\mathrm{mW}]}{1000}=P[\mathrm{W}]=\frac{V_{rms}^2}{R}=\frac{(V_{pp}/\sqrt{2})^2}{R}=\frac{V_{pp}^2}{2R}=\frac{V_{pp}^2}{2*50}=\frac{V_{pp}^2}{100}=\frac{V_{rms}^2}{50}

\frac{P[\mathrm{mW}]}{1000}=\frac{V_{pp}^2}{100}=\frac{V_{rms}^2}{50}

P[\mathrm{mW}]=\frac{1000V_{pp}^2}{100}=\frac{1000V_{rms}^2}{50}

P[\mathrm{mW}]=10V_{pp}^2=20V_{rms}^2

\mathrm{dBmW}=\mathrm{dB}(P[\mathrm{mW}])=\mathrm{dB}\left(10V_{pp}^2\right)=\mathrm{dB}\left(20V_{rms}^2\right)

\mathrm{dBmW}=\mathrm{dB}\left({V_{pp}^2}\right)+10\mathrm{dB}=\mathrm{dB}\left({V_{rms}^2}\right)+13\mathrm{dB}

\mathrm{dBmW}=20\log_{10}\left({V_{pp}}\right)+10=20\log_{10}\left({V_{rms}}\right)+13

This is all simple middle school math made very complicated and scary by people who abuse notations and the context are lost in translation, yet nobody really took the time in engineering school to figure out and explain why things are what they are. People just wanted to follow rules instead of sitting down and derive the rationale whenever they came across something not intuitively obvious.

Rambling Nerd with a Plan

Hoi Wong's blog