Start with an example lambda calculus expression . It is:

• [programming view] a function with 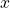as an input argument and it uses 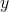from the outer workspace (called a free-variable). f(var x) { return y+x; }
• [mathematical view] can also be written as 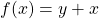where 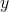is seen as a fixed/snapshotted value relative to the expression.

g(int y) => (int x) => y + x

Lambda calculus is right-associative

g(int y) => ( (int x) => y + x )

Unrolling in C-style it will give better insights to the relationships between layers

g(int y) {
  return (int x) { return y + x; };
}

Note that (int x) { return y + x; } is a functor. To emphasize this, the same code can be rewritten by assigning the name f to it and returning f:

g(int y) {
  f(int x) { return y + x; };
  return f;
}

Use the C++11 style syntax so that it doesn’t look like nested function implementation body instead of a functor nested inside a function:

g(int y) {
  var f = (int x) { return y + x; };
  return f;
}

Note that conceptually what we are doing with the wrapper cascade is indeed nested functions. However, in the wrapper, we spit out a functor (which did most of the partial work) so the user can endow/evaluating it with the last piece of needed info/input:

g(int y) {
  f(int x) { 
   return y + x;
  };
  return f;
}

More commonly as seen in Dart docs, this formatting shows a (binder/capturing) wrapper function returning its own nested function:

g(int y) {
  return (int x) { 
           return y + x;
         };
}